Наиболее рационально строить модель функционирования системы по блочному принципу.
При этом могут быть выделены три автономные группы блоков такой модели.
- Блоки первой группы представляют собой имитатор воздействий внешней среды Е на систему S;
- блоки второй группы являются собственно моделью процесса функционирования исследуемой системы S;
- блоки третьей группы — вспомогательными и служат для машинной реализации блоков двух первых групп, а также для фиксации и обработки результатов моделирования.
Рассмотрим механизм перехода от описания процесса функционирования некоторой гипотетической системы к модели этого процесса [29, 35]. Для наглядности введем представление об описании свойств процесса функционирования системы S, т. е. об ее концептуальной модели Мт как совокупности некоторых элементов, условно изображенных квадратами так, как показано на рис. 3.2, а. Эти квадраты представляют собой описание некоторых подпроцессов исследуемого процесса функционирования системы S, воздействия внешней среды Е и т. д. Переход от описания системы к ее модели в этой интерпретации сводится к исключению из рассмотрения некоторых второстепенных элементов описания (элементы 5 — 8,39 — 41,43 — 47).
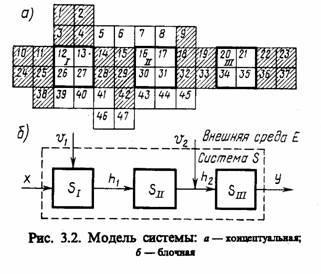
Предполагается, что они не оказывают существенного влияния на ход процессов, исследуемых с помощью модели. Часть элементов (14, 15, 28, 29, 42) заменяется пассивными связями hl3отражающими внутренние свойства системы (рис. 3.2, б). Некоторая часть элементов (1 — 4, 10, 11, 24, 25) заменяется входными факторами х и воздействиями внешней среды v1. Возможны и комбинированные замены: элементы 9, 18, 19, 32, 33 заменены пассивной связью h2 и воздействием внешней среды Е. Элементы 22, 23,36,37 отражают воздействие системы на внешнюю средуу.
Оставшиеся элементы системы S группируются в блоки 5t, Sa, Sm, отражающие процесс функционирования исследуемой системы. Каждый из этих блоков достаточно автономен, что выражается в минимальном количестве связей между ними. Поведение этих блоков должно быть хорошо изучено и для каждого из них построена математическая модель, которая в свою очередь может содержать ряд подблоков. Построенная блочная модель процесса функционирования исследуемой системы 5 предназначена для анализа характеристик этого процесса, который может быть проведен при машинной реализации полученной модели.